ML estimatoren resulterer i verdien for parameteren som mest sannsynlig vil forekomme i datasettet.

Gitt forutsetningene, er ML estimatoren verdien av parameteren som har den beste sjansen for å produsere datasettet.

Jeg kan ikke intuitivt forstå en partisk ML-estimator i den forstand at "Hvordan kan den mest sannsynlige verdien for parameteren forutsi den virkelige verdien til parameteren med en skjevhet mot en feil verdi? "

Skjevhet handler om forventninger om samplingsfordelinger. "Mest sannsynlig å produsere dataene" handler ikke om forventningene til distribusjon av prøvetaking. Hvorfor forventes det at de går sammen?

Hva er grunnlaget det er overraskende at de ikke nødvendigvis samsvarer med?

Jeg vil foreslå at du vurderer noen enkle tilfeller av MLE og tenk på hvordan forskjellen oppstår i de spesielle tilfellene.

Som et eksempel kan du vurdere observasjoner på uniform på $ (0, \ theta) $ . Den største observasjonen er (nødvendigvis) ikke større enn parameteren, så parameteren kan bare ta verdier som er minst like store som den største observasjonen.

Når du vurderer sannsynligheten for $ \ theta $ , det er (åpenbart) større jo nærmere $ \ theta $ er den største observasjonen. Så det er maksimert at den største observasjonen; det er tydeligvis estimatet for $ \ theta $ som maksimerer sjansen for å få prøven du fikk:

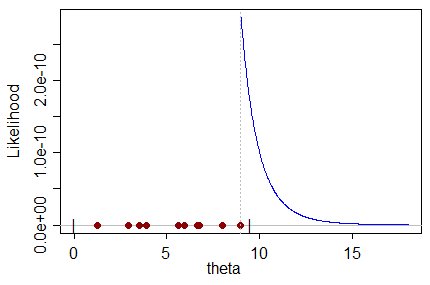
Men på den annen side må det være partisk, siden den største observasjonen åpenbart (med sannsynlighet 1) er mindre enn den sanne verdien av $ \ theta $ ; ethvert annet estimat av $ \ theta $ som ikke allerede er utelukket av selve prøven, må være større enn det, og må (ganske tydelig i dette tilfellet) være mindre sannsynlig å produsere prøven.

Forventningen om den største observasjonen fra en $ U (0, \ theta) $ er $ \ frac {n } {n + 1} \ theta $ , så den vanlige måten å uklare er å ta som estimator for $ \ theta $ : $ \ hat \ theta = \ frac {n + 1} {n} X _ {(n)} $ , der $ X _ {( n)} $ er den største observasjonen.

Dette ligger til høyre for MLE, og har så lavere sannsynlighet.

$ \ beta ^ {MLE} $ er ikke den mest sannsynlige verdien av $ \ beta $. Den mest sannsynlige verdien er $ \ beta $ selv. $ \ beta ^ {MLE} $ maksimerer sannsynligheten for å tegne prøven vi faktisk fikk.

MLE er bare asymptotisk upartisk, og ofte kan du justere estimatoren for å oppføre seg bedre i endelige prøver. For eksempel er MLE for variansen til en tilfeldig variabel et eksempel, der multiplisering med $ \ frac {N} {N-1} $ transformerer den.

Her er intuisjonen min.

Bias er et mål på nøyaktighet , men det er også en forestilling om presisjon .

I en ideell verden ville vi få estimatet, som er både presist og nøyaktig, dvs. alltid treffer øyeøyet. Dessverre, i vår ufullkomne verden, må vi balansere nøyaktighet og presisjon. Noen ganger kan vi føle at vi kan gi litt nøyaktighet for å få mer presisjon: vi bytter hele tiden. Derfor betyr det faktum at en estimator er partisk, ikke at den er dårlig: det kan være at den er mer presis.

Vanlige språklige og tekniske betydninger av partisk er forskjellige. Svaret fra @Glen_b gir en god beskrivelse av hvorfor estimatorer for maksimal sannsynlighet lett kan være partisk i teknisk forstand.

Det er mulig at estimatoren for maksimal sannsynlighet er partisk i noe som vanlig språk, men det er ikke vanlig. Noe må gå galt.

Standardeksemplene på en inkonsekvent MLE involverer sammenkoblede data.

Anta $ X_ {ij} \ sim N (\ mu_i, \ sigma ^ 2) $ , for $ j = 0,1 $ og $ i = 1,2,3, \ dots, n $ . MLE for $ \ mu_i $ er $ (X_ {i0} + X_ {i1}) / 2 $ span >. MLE for $ \ hat \ sigma ^ 2 $ er $$ \ hat \ sigma ^ 2 = \ frac {1} {2n} \ sum_ {i = 1} ^ n \ sum_ {j = 0} ^ 1 (X_ {ij} - \ hat \ mu_i) ^ 2 $$

Når du får mer data, $ \ hat \ sigma ^ 2 $ konvergerer ikke til $ \ sigma ^ 2 $ men til $ \ sigma ^ 2/2 $ .

Med binære matchede pardata er genereringsmodellen $$ \ mathrm {logit} \, P [Y_ {ij} = 1] = \ alpha_i + \ beta \ times j $ $ MLE $ \ hat \ beta $ konvergerer til $ 2 \ beta $ i stedet for til $ \ beta $ .

I begge tilfeller er problemet at antall parametere vokser med $ n $ , og løsningen er en betinget sannsynlighet som fjerner $ n $ avskjærer parametere før du estimerer parameteren du er interessert i.