Spørsmål:
Hva er forskjellen mellom ZCA-bleking og PCA-bleking?
RockTheStar
2014-10-01 12:22:41 UTC
view on stackexchange narkive permalink

Jeg er forvirret om ZCA-bleking og normalbleking (som oppnås ved å dele hovedkomponenter med kvadratrøttene til PCA egenverdier). Så vidt jeg vet,

$$ \ mathbf x_ \ mathrm {ZCAwhite} = \ mathbf U \ mathbf x_ \ mathrm {PCAwhite}, $$ hvor $ \ mathbf U $ er PCA egenvektorer.

Hva bruker ZCA-bleking? Hva er forskjellene mellom normalbleking og ZCA-bleking?

I følge "Neural Networks: Tricks of the Trade", skiller PCA og ZCA seg bare ved en rotasjon.
To svar:
amoeba
2014-10-01 17:49:14 UTC
view on stackexchange narkive permalink

La (sentrerte) data lagres i en $ n \ ganger d $ matrise $ \ mathbf X $ med $ d $ funksjoner (variabler) i kolonner og $ n $ datapunkter i rader. La kovariansmatrisen $ \ mathbf C = \ mathbf X ^ \ top \ mathbf X / n $ ha egenvektorer i kolonner på $ \ mathbf E $ og egenverdier på diagonalen til $ \ mathbf D $, slik at $ \ mathbf C = \ mathbf E \ mathbf D \ mathbf E ^ \ top $.

Så det du kaller "normal" PCA-blekingstransformasjon er gitt av $ \ mathbf W_ \ mathrm {PCA} = \ mathbf D ^ {- 1/2} \ mathbf E ^ \ top $, se f.eks mitt svar i Hvordan bleke dataene ved hjelp av hovedkomponentanalyse?

Denne blekingstransformasjonen er imidlertid ikke unik. Faktisk vil hvite data forbli hvite etter enhver rotasjon, noe som betyr at enhver $ \ mathbf W = \ mathbf R \ mathbf W_ \ mathrm {PCA} $ med ortogonal matrise $ \ mathbf R $ også vil være en blekingstransformasjon. I det som kalles ZCA-bleking tar vi $ \ mathbf E $ (stablet sammen egenvektorer av kovariansmatrisen) som denne ortogonale matrisen, dvs. $$ \ mathbf W_ \ mathrm {ZCA} = \ mathbf E \ mathbf D ^ {- 1 / 2} \ mathbf E ^ \ top = \ mathbf C ^ {- 1/2}. $$

En definerende egenskap for ZCA-transformasjon ( noen ganger også kalt "Mahalanobis transformation ") er at det resulterer i hvite data som er så nær som mulig de opprinnelige dataene (i minste firkant). Med andre ord, hvis du vil minimere $ \ | \ mathbf X - \ mathbf X \ mathbf A ^ \ top \ | ^ 2 $ med forbehold om at $ \ mathbf X \ mathbf A ^ \ top $ blir bleket, så bør du ta $ \ mathbf A = \ mathbf W_ \ mathrm {ZCA} $. Her er en 2D-illustrasjon:

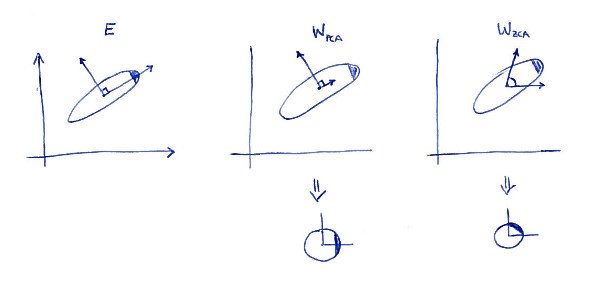
PCA and ZCA whitening

Venstre delplott viser dataene og hovedaksene. Legg merke til den mørke skyggen i det øvre høyre hjørnet av fordelingen: den markerer retningen. Rader med $ \ mathbf W_ \ mathrm {PCA} $ vises på den andre delplottet: dette er vektorene dataene projiseres på. Etter bleking (nedenfor) ser fordelingen seg rundt, men legg merke til at den også ser rotert ut --- mørkt hjørne er nå på østsiden, ikke på nordøstsiden. Rader med $ \ mathbf W_ \ mathrm {ZCA} $ vises på den tredje delplottet (merk at de ikke er ortogonale!). Etter bleking (under) ser distribusjonen rundt og den er orientert på samme måte som opprinnelig. Selvfølgelig kan man komme fra PCA-hvite data til ZCA-hvite data ved å rotere med $ \ mathbf E $.

Begrepet "ZCA" ser ut til å ha blitt introdusert i Bell og Sejnowski 1996 i sammenheng med uavhengig komponentanalyse, og står for "zero-phase component analysis". Se der for mer informasjon. Mest sannsynlig kom du over dette begrepet i sammenheng med bildebehandling. Det viser seg at når de brukes på en haug med naturlige bilder (piksler som funksjoner, hvert bilde som datapunkt), ser hovedaksene ut som Fourier-komponenter med økende frekvenser, se første kolonne i figur 1 nedenfor. Så de er veldig "globale". På den annen side ser rader med ZCA-transformasjon veldig "lokale" ut, se den andre kolonnen. Dette er nettopp fordi ZCA prøver å transformere dataene så lite som mulig, og slik at hver rad bedre bør være nær en av de opprinnelige basisfunksjonene (som ville være bilder med bare en aktiv piksel). Og dette er mulig å oppnå, fordi korrelasjoner i naturlige bilder for det meste er veldig lokale (så de-korrelasjonsfiltre kan også være lokale).

PCA and ZCA in Bell and Sejnowski 1996

Oppdater

Flere eksempler på ZCA-filtre og bilder transformert med ZCA er gitt i Krizhevsky, 2009, Learning Multiple Layers of Features from Tiny Images, se også eksempler i @ bayerj's svar (+1).

Jeg tror disse eksemplene gir en ide om når ZCA-bleking kan være å foretrekke fremfor PCA-en. ZCA-hvite bilder ligner nemlig fremdeles på normale bilder mens PCA-hvite bilder ikke ser ut som normale bilder. Dette er sannsynligvis viktig for algoritmer som nevrale nettverk av konvolusjon (som f.eks. Brukt i Krizhevskys papir), som behandler nabopiksler sammen og i så stor grad er avhengige av de lokale egenskapene til naturlige bilder. For de fleste andre maskinlæringsalgoritmer bør det være absolutt irrelevant om dataene blir bleket med PCA eller ZCA.

Takk!Jeg har et spørsmål: så betyr det at ZCA i utgangspunktet endrer tilgangen, men ikke endrer posisjonen til dataene mye?(basert på skyggeleggingsområdet).Er det også middel når vi gjør bleking, bør vi gjøre ZCA-bleking?Hvordan bestemmer vi oss for å bruke PCAwhitening eller ZCA whitening?
(1) Jeg er ikke helt sikker på hva du mener, men jeg vil si det slik: ZCA strekker datasettet for å gjøre det sfærisk, men * prøver ikke å rotere det * (mens PCA roterer det ganske mye).(2) Jeg tror faktisk at det i de fleste tilfeller ikke betyr noe om du bruker PCA eller ZCA-bleking.Den eneste situasjonen jeg kan forestille meg hvor ZCA kan være å foretrekke, er forbehandling for konvolusjonelle nevrale nettverk.Vennligst se en oppdatering av svaret mitt.
@amoeba Hva betyr det å ta en matrise til kraften -1/2?
@power For den diagonale matrisen ($ \ mathbf D $ i dette svaret) betyr det ganske enkelt å heve hvert diagonale element til kraften $ -1 / 2 $.For en kovariansmatrise $ \ mathbf C = \ mathbf E \ mathbf D \ mathbf E ^ \ top $ kan vi definere den som $ \ mathbf E \ mathbf D ^ {- 1/2} \ mathbf E ^ \ top $.
Jeg er litt forvirret av den siste grafikken.Hva betyr det?Det er en ting å plotte de første hovedkomponentene, men etter ZCA-bleking er det ingen "komponenter", du kan bare se på hvordan et bilde ser ut etter bleking.Eller kanskje etter å ha blekt, og behold bare de få første komponentene.Men uansett, bør du sammenligne dette med bildene rekonstruert fra PCA, ikke med selve hovedkomponentene, det gir ikke mening.Så hva betyr det uansett? ...
@dividebyzero Det er bare rader med $ W $ (hver rad, dvs. hver PCA egenvektor eller hver ZCA-projiserende vektor, er avbildet som et bilde).Du kan si at det * er * "komponenter" etter ZCA, hvorfor ikke.
PCA er som å lage en Fourier-transform, ZCA er som å transformere, multiplisere og transformere tilbake, ved å bruke et (null-fase) lineært filter.Så det vi ser der er filterimpulsresponsen ved hver piksel."Komponentene" som er involvert i operasjonen er de samme, kolonnene i E, som er "hovedkomponentene" ... Jeg mener, du kan også kalle radene med W-komponenter, men jeg tror det er viktig å forstå atsamme "hovedkomponenter" er involvert, og når du bruker ZCA er du tilbake på det opprinnelige domenet, mens du med PCA må "rekonstruere" signalet.
@dividebyzero +1 til din siste kommentar, jeg tror dette er et verdifullt perspektiv.Uansett håper jeg betydningen av min siste figur (som er hentet fra det sammenhengende papiret) er klar nå.
Sikker.Jeg måtte gå etter papiret for å virkelig forstå det.Det opprinnelige bildet har mye mer informasjon, så jeg anbefaler alle som leser dette å gå etter det! ... Takk for den flotte referansen, btw.:)
Jeg er ikke så sikker på "ZCA-hvite bilder ligner vanlige bilder; PCA-hvite bilder ikke gjør det".http://ufldl.stanford.edu/tutorial/unsupervised/ExercisePCAWhitening/ Der ser vi at PCA-bilder og ZCA-bilder begge ser ut som MNIST-tall.Jeg kan i teorien se hva du sier, men jeg antar at jeg ikke kan se det empirisk.
@learning Du ser ikke PCA-hvite bilder på den siden!De viser "PCA dimensjonsreduserte bilder", dvs. * rekonstruksjoner * via PCA, men ikke PCA-projeksjoner selv.
@amoeba Hvordan kan man bevise at ZCA er gitt ved "minimering av $ ∥X − XA ^ \ top∥ ^ 2 $ underlagt $ XA ^ \ top $ ble bleket"?
"hvite data vil forbli hvite etter en rotasjon" hvorfor er dette sant?$ Cov (RX) = RCov (X) R ^ T $ Dette trenger ikke å være diagonalt selv om $ Cov (X) $ er diagonalt og $ R $ er ortogonal
Ah jeg ser det er fordi $ Cov (X) $ er identitet ikke bare diagonalt
bayerj
2014-10-01 17:35:27 UTC
view on stackexchange narkive permalink

Gitt en Eigendekomposisjon av en kovariansematrise $$ \ bar {X} \ bar {X} ^ T = LDL ^ T $$ hvor $ D = \ text {diag} (\ lambda_1, \ lambda_2, \ dots, \ lambda_n) $ er den diagonale matrisen til Eigenvalues, vanlig bleking for å transformere dataene til et rom der kovariansmatrisen er diagonal: $$ \ sqrt {D ^ {- 1}} L ^ {- 1} \ bar {X} \ bar {X} ^ TL ^ {- T} \ sqrt {D ^ {- 1}} = \ sqrt {D ^ {- 1}} L ^ {- 1} LDL ^ TL ^ {- T} \ sqrt { D ^ {- 1}} \\ = \ mathbf {I} $$ (med noe misbruk av notasjon.) Det betyr at vi kan diagonalisere kovariansen ved å transformere dataene i henhold til $$ \ tilde {X} = \ sqrt {D ^ {- 1}} L ^ {- 1} X. $$

Dette er vanlig bleking med PCA. Nå gjør ZCA noe annet - det legger til en liten epsilon til Eigenvalues ​​og forvandler dataene tilbake. $$ \ tilde {X} = L \ sqrt {(D + \ epsilon) ^ {- 1}} L ^ {- 1} X. $$ Her er noen bilder fra CIFAR-datasettet før og etter ZCA.

Før ZCA:

before ZCA

Etter ZCA med $ \ epsilon = 0,0001 $

after ZCA 1e-4

Etter ZCA med $ \ epsilon = 0,1 $

after ZCA with .1

For visjonsdata, vil høyfrekvente data vanligvis ligge i rommet som spennes av de lavere Eigenvalues. Derfor er ZCA en måte å styrke disse på, noe som fører til mer synlige kanter osv.

Bør ikke epsilonen legges til før du tar invers?Jeg tror det bare er lagt til for å stabilisere inversjonen i tilfelle nesten null egenverdier.Så hvis det er fornuftig å legge det til for ZCA-bleking, ville det være fornuftig å legge det til for PCA-bleking også.
Ja, før det omvendte, takk.Siden dette vanligvis gjøres med SVD i praksis, vet jeg ikke om det er nødvendig å stabilisere inversjonen.
Jeg har lagt til et nytt bilde for å vise effekten.
+1, men jeg har en rekke ytterligere spørsmål og spørsmål.(1) Det jeg mente om epsilon er at det ikke er spesifikt for ZCA, det kan også brukes til PCA-bleking.(2) Jeg er ikke sikker på at jeg forstår din kommentar om SVD: SVD eller ikke, man trenger å invertere entallverdier, derav behovet for epsilon.(3) PCA-blekingstransformasjon er $ D ^ {- 1/2} L ^ \ top $, du skrev den omvendt, og dette gjør beregningen i den andre formelen feil ... (4) Fine figurer, hvorer de fra?(5) Vet du i hvilke situasjoner ville ZCA-bleking være å foretrekke fremfor PCA-bleking, og hvorfor?
(1) avtalt.Jeg har ingen intuisjon om hva det betyr.(2) Min spaltningskunnskap er ufullstendig her, men jeg antok at en klassisk inversjonsmatrise på en entallskovariansmatrise vil mislykkes, mens SVD på en datamatrise som gir opphav til en entallskovarians ikke vil.(3) Takk, vil fikse det.(4) Fra koden min :) (5) Jeg antar at det for mange algoritmer som gir overkomplette representasjoner (f.eks. GainShape K-midler, Auto-kodere, RICA) og / eller gjør en lignende jobb som PCA algebraisk uavhengighet av funksjonene gjør vondt, menJeg har ingen hard kunnskap om dette.
(1-2) Tenk på en matrise med en veldig liten entallverdi.Kovariansmatrisen har en veldig liten egenverdi.Enten du bruker SVD på X eller EIG på XX ', må denne verdien inverteres - forsterker i stor grad støyen.Jeg er ganske sikker på at dette er begrunnelsen bak epsilon.(4) Hyggelig :) (5) Ikke sikker på at jeg forstår: hva mener du med "algebraisk uavhengighet av funksjonene" og hvorfor skulle PCA-bleking føre til det og ZCA-bleking ikke?Jeg har en annen hypotese, men jeg har nettopp oppdatert svaret mitt med det.
(1-2) Takk!(5) Algebraisk uavhengighet av funksjoner er forskjellig fra statistisk uavhengighet av varians, dvs. $ w_i ^ Tw_j = 0 $.I utgangspunktet ortogonalt, så hva PCA gjør.Siden du tok opp temaet dype garn: frafall er også kjent for å fungere ekstremt dårlig på PCA-data - noen funksjoner er overflødige.
Høres interessant ut, men jeg forstår det fremdeles ikke: om du bruker PCA eller ZCA for å bleke dataene, blir det bleket til slutt!Det betyr at funksjoner har null korrelasjon, dvs. ingen funksjonsredundans.Hvis du sier at funksjoner kan være uavhengige selv om de har null korrelasjon, så er det selvfølgelig riktig, men jeg ser ikke hvordan PCA og ZCA-bleking skiller seg ut med hensyn til ikke-lineære avhengigheter mellom funksjonene.Tross alt er ZCA-bleking bare en rotasjon av PCA, ingenting mer!
Regulariseringen av denoising / kontraktive autokodere og frafall er avhengig av aksene til inngangen.Dermed hvis du forstyrrer hovedkomponenten, vil et nettverk med injisert støy ikke kunne komme seg fra det siden den informasjonen mangler overalt ellers.Disse algoritmene er robuste mot støy som er uavhengig av hver komponent ved å velge å se på mange forskjellige av dem som koder for den samme informasjonen, men med ulik støy.Denne antagelsen er gyldig i mange sensoriske felt, for eksempel lyd og bilde.


ⓘ
Denne spørsmålet ble automatisk oversatt fra engelsk.Det opprinnelige innholdet er tilgjengelig på stackexchange, som vi takker for cc by-sa 3.0-lisensen den distribueres under.
Loading...