Absolutt kan gjennomsnittet pluss en sd overstige den største observasjonen.

Tenk på prøven 1, 5, 5, 5 -

den har gjennomsnitt 4 og standardavvik 2, så gjennomsnittet + sd er 6, en mer enn prøven maksimalt. Her er beregningen i R:

  > x = c (1,5,5,5) > mean (x) + sd (x) [1] 6  

Det er en vanlig forekomst. Det har en tendens til å skje når det er en rekke høye verdier og en hale til venstre (dvs. når det er sterk venstre skjevhet og en topp nær maksimum).

-

The samme mulighet gjelder for sannsynlighetsfordelinger, ikke bare prøver - populasjonsgjennomsnittet pluss populasjonen sd kan lett overstige den maksimalt mulige verdien.

Her er et eksempel på en $ \ text {beta} (10, \ frac {1} {2}) $ tetthet, som har en maksimal mulig verdi på 1:

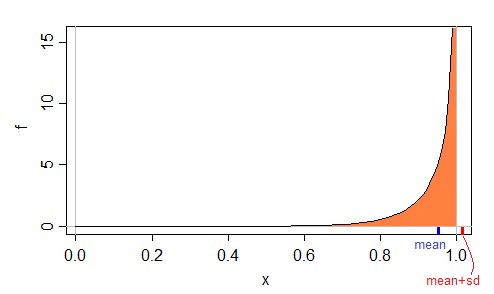
I dette tilfellet kan vi se på Wikipedia-siden for beta-distribusjon, som sier at gjennomsnittet er:

$ \ operatorname {E} [X] = \ frac {\ alpha} {\ alpha + \ beta} \! $

og avviket er:

$ \ operatorname {var} [X] = \ frac {\ alpha \ beta } {(\ alpha + \ beta) ^ 2 (\ alpha + \ beta + 1)} \! $

(Selv om vi ikke trenger å stole på Wikipedia, siden de er ganske enkle å utlede.)

Så for $ \ alpha = 10 $ og $ \ beta = \ frac {1} {2} $ har vi gjennomsnitt $ \ ca 0,9523 $ og sd $ \ ca 0,0628 $, så betyr + sd $ \ omtrent 1.0152 $, mer enn det mulige maksimum på 1.

Det vil si at det er lett mulig å ha en verdi på middel + sd som ikke kan observeres som en dataverdi .

--

For alle situasjoner der modusen var maksimalt, må Pearson-modus skjevhet bare være $ < \, - 1 $ for gjennomsnitt + sd for å overskride maksimumet. Det kan ta hvilken som helst verdi, positiv eller negativ, slik at vi kan se at det er lett mulig.

-

Et nært beslektet problem blir ofte sett med konfidensintervaller for et binomium andel, der et ofte brukt intervall, kan det normale tilnærmelsesintervallet produsere grenser utenfor $ [0,1] $.

Vurder for eksempel et normalt tilnærmelsesintervall på 95,4% for populasjonsandelen suksesser i Bernoulli-studier (utfallet er henholdsvis 1 eller 0 som representerer suksess og fiaskohendelser), hvor 3 av 4 observasjoner er "$ 1 $" og en observasjon er "$ 0 $".

Da er den øvre grensen for intervallet $ \ hat p + 2 \ ganger \ sqrt {\ frac {1} {4} \ hat p \ left (1 - \ hat p \ right)} = \ hat p + \ sqrt {\ hat p (1 - \ hat p)} = 0,75 + 0,433 = 1,183 $

Dette er bare eksemplets gjennomsnitt + det vanlige estimatet for sd for binomialet ... og produserer en umulig verdi.

Den vanlige prøven sd for 0,1,1,1 er 0,5 i stedet for 0,433 (de skiller seg ut fordi det binomiale ML-estimatet av standardavviket $ \ hat p (1- \ hat p) $ tilsvarer å dele variansen med $ n $ i stedet for $ n-1 $). Men det gjør ingen forskjell - i begge tilfeller overstiger middel + sd størst mulig andel.

Dette faktum - at et normalt tilnærmingsintervall for binomialet kan produsere "umulige verdier" blir ofte notert i bøker og papirer . Imidlertid har du ikke å gjøre med binomial data. Likevel er problemet - det betyr + et visst antall standardavvik ikke en mulig verdi - analogt.

-

I ditt tilfelle er den uvanlige "0" -verdien i prøven din gjør sd stort mer enn det trekker gjennomsnittet ned, og derfor er middel + sd høyt.

-

( Spørsmålet ville i stedet være - med hvilken begrunnelse ville det være umulig? - for uten å vite hvorfor noen tror det er et problem i det hele tatt, hva tar vi for oss?)

Logisk selvfølgelig viser man at det er mulig ved å gi et eksempel der det skjer. Du har allerede gjort det. I mangel av en oppgitt grunn til at det skulle være annerledes, hva skal du gjøre?

Hvis et eksempel ikke er tilstrekkelig, hvilket bevis vil da være akseptabelt?

Det er egentlig ikke noe poeng å bare peke på en uttalelse i en bok, siden enhver bok kan uttale seg feilaktig - jeg ser dem hele tiden. Man må stole på direkte demonstrasjon av at det er mulig, enten et bevis i algebra (man kan konstruere fra betaeksemplet ovenfor for eksempel *) eller ved numerisk eksempel (som du allerede har gitt), som alle kan undersøke sannheten om selv .

* whuber gir de nøyaktige forholdene for beta-saken i kommentarer.

Per Chebyshevs ulikhet kan mindre enn k ^-2 poeng være mer enn k standardavvik unna. Så for k = 1 betyr det at mindre enn 100% av prøvene dine kan være mer enn ett standardavvik.

Det er mer interessant å se på lavgrensen. Professoren din bør være mer overrasket over at det er poeng som er omtrent 2,5 standardavvik under gjennomsnittet. Men vi vet nå at bare omtrent 1/6 av prøvene dine kan være 0.

Essensen av problemet kan være at distribusjonen din ikke er en normalfordeling som et standardavvik antar. Distribusjonen din er sannsynligvis venstre skjev, så du må først transformere settet ditt til en normalfordeling ved å velge en passende transformasjonsfunksjon. Denne prosessen kalles transformasjon til normalitet. En slik funksjonskandidat i ditt tilfelle kan være en speilet loggtransformasjon. Når settet ditt oppfyller en normalitetstest, kan du ta standardavviket. For å bruke 1 $ \ sigma $ eller 2 $ \ sigma $ verdiene må du forvandle dem tilbake til det opprinnelige datarommet ved hjelp av det omvendte av transformasjonsfunksjonen. Jeg tenker at dette er det professoren din antydet.

Generelt for tilfeldige variabler i Bernoulli $ X $, som tar verdien $ 1 $ med sannsynligheten $ 0<p<1 $ og verdien $ 0 $ med sannsynligheten $ 1-p $, har vi

$$ E ( X) = p, \; \; SE (X) = \ sqrt {p (1-p)} $$

Og vi vil

$$ E (X) + SE (X) > 1 \ Rightarrow p + \ sqrt {p (1-p)} >1 $$

$$ \ Rightarrow \ sqrt {p (1-p)} > (1-p) $$

Firkant begge sider for å få

$$ p (1-p) > (1-p) ^ 2 \ Rightarrow p > 1-p \ Rightarrow p > \ frac 12 $$

Med ord, for hvilken som helst Bernoulli tilfeldig variabel med $ p>1 / 2 $, holder det teoretiske uttrykket $ E (X) + SE (X) > \ max X $.

Så for eksempel for ethvert ID prøve hentet fra en Bernoulli med for eksempel $ p = 0,7 $, i de fleste tilfeller vil prøven gjennomsnitt pluss prøven standardavviket overstige verdien $ 1 $, som vil være den maksimale verdien som er observert (sperre tilfellet med en null-prøve!).

For andre fordelinger har vi alltid motsatt retning i ulikheten, f.eks. for en enhetlig $ U (a, b) $ er det alltid slik at $ E (U) + SE (U) < \ max U = b $.
Det eksisterer derfor ingen generell regel.